分子轨道理论

叫个啥名字发布于 2022-5-27 16:03 阅读：697 理论化学

分子轨道实际上就是一种近似处理，原子轨道线性组合形成分子轨道那就是进一步近似。核心在于Slater行列式和变分法。

单电子系统的薛定谔方程与分子轨道

对于单电子系统，做BO近似冻结原子核的运动，再扣除原子核之间的排斥能，于是就只剩下动能项和核与电子的吸引项，因此可以写出薛定谔方程（已使用原子单位）：

$(-\frac12\nabla^2-\sum^{N}_{a=1}\frac{Z_a}{r_{a}})\psi=\varepsilon\psi$

其中 $r_{a}$ 是电子与原子 $a$ 的距离。该方程的解就是单电子系统的分子轨道。

变分法：用原子轨道的线性组合近似分子轨道

虽然像氢分子离子 $\ce{H_2+}$ 可以精确求解其分子轨道，但是对于更大的系统我们却无能为力了。我们可以用一组原子轨道 $\{\phi_i\}$ 的线性组合近似分子轨道 $\psi$ ：

$\psi=\sum_{i=1}^nc_i\phi_i$

这种近似效果如何呢？变分原理告诉我们，任何一个符合边界条件的试探波函数的能量，总是不小于基态能量：

$E=\left<\Psi\right|\hat H\left|\Psi\right>\geq\varepsilon_0$

那么，调整系数 $\{c_i\}$ ，使得 $E$ 的能量最小，就可以得到真实基态波函数的最佳近似。

这将化为久期行列式的求解（证明见附录）：

$\det{(\bold H-E\bold S)}=0$

$\begin{vmatrix}H_{11}-E&H_{12}-ES_{12}&\cdots&H_{1n}-ES_{1n}\\H_{21}-ES_{21}&H_{22}-E&\cdots&H_{2n}-ES_{2n}\\\vdots&\vdots&\ddots&\vdots\\ H_{n1}-ES_{n1}&H_{n2}-ES_{n2}&\cdots&H_{nn}-E \end{vmatrix}=0$

其中， $S_{ij}=\left<\phi_i|\phi_j\right>$ ， $H_{ij}=\left<\phi_i\right |\hat H\left |\phi_j\right>$ .

久期行列式可以解出 $n$ 个 $E$ 来，这实际上是 $E$ 的 $n$ 个极值，还可以证明，这些 $E_i$ 分别对应第 $i$ 个本征能量的上界：（证明见附录）

$E_i\geq\varepsilon_i,\quad i=0,1,2,...,n-1$

所以说用原子轨道的线性组合近似分子轨道是可行的。

实际上我们不必用准确的原子轨道作为基函数，对于原子轨道也可以进一步近似，这将衍生出基组的概念。

实例1：分子轨道理论处理氢分子离子

设 $\phi_1$ 、 $\phi_2$ 是两个氢原子的1s轨道，因此线性组合成分子轨道：

$\psi=c_1\phi_1+c_2\phi_2$

解久期行列式：

$\begin{vmatrix}H_{11}-E&H_{12}-ES_{12}\\H_{12}-ES_{12}&H_{22}-E \end{vmatrix}=0$

因为有 $H_{11}=H_{12}$ ，得到

$E_1=\frac{H_{11}+H_{12}}{1+S_{12}}=E_\ce H+\frac{J+K}{1+S_{12}}$

$E_{2}=\frac{H_{11}-H_{12}}{1-S_{12}}=E_\ce H+\frac{J-K}{1-S_{12}}$

最后一步用到了：

$H_{11}=\left<\phi_1\right |\hat H\left |\phi_1\right>=\left<\phi_1\right |-\frac12\nabla^2-\frac{1}{r_{1}}\left |\phi_1\right>+\left<\phi_1\right |-\frac{1}{r_{2}}\left |\phi_1\right>=E_\ce H+J$

$H_{12}=\left<\phi_1\right |\hat H\left |\phi_2\right>=\left<\phi_1\right |-\frac12\nabla^2-\frac{1}{r_{1}}\left |\phi_2\right>+\left<\phi_1\right |-\frac{1}{r_{2}}\left |\phi_2\right>=E_\ce HS_{12}+K$

其中 $S_{12}$ 、 $J$ 、 $K$ 皆与核间距 $R$ 有关：

$S_{12}=(1+R+\frac{R^2}{3})e^{-R}$

$J=-\frac1R+(1+\frac1R)e^{-2R}$

$K=-(1+R)e^{-R}$

给大家画个图：

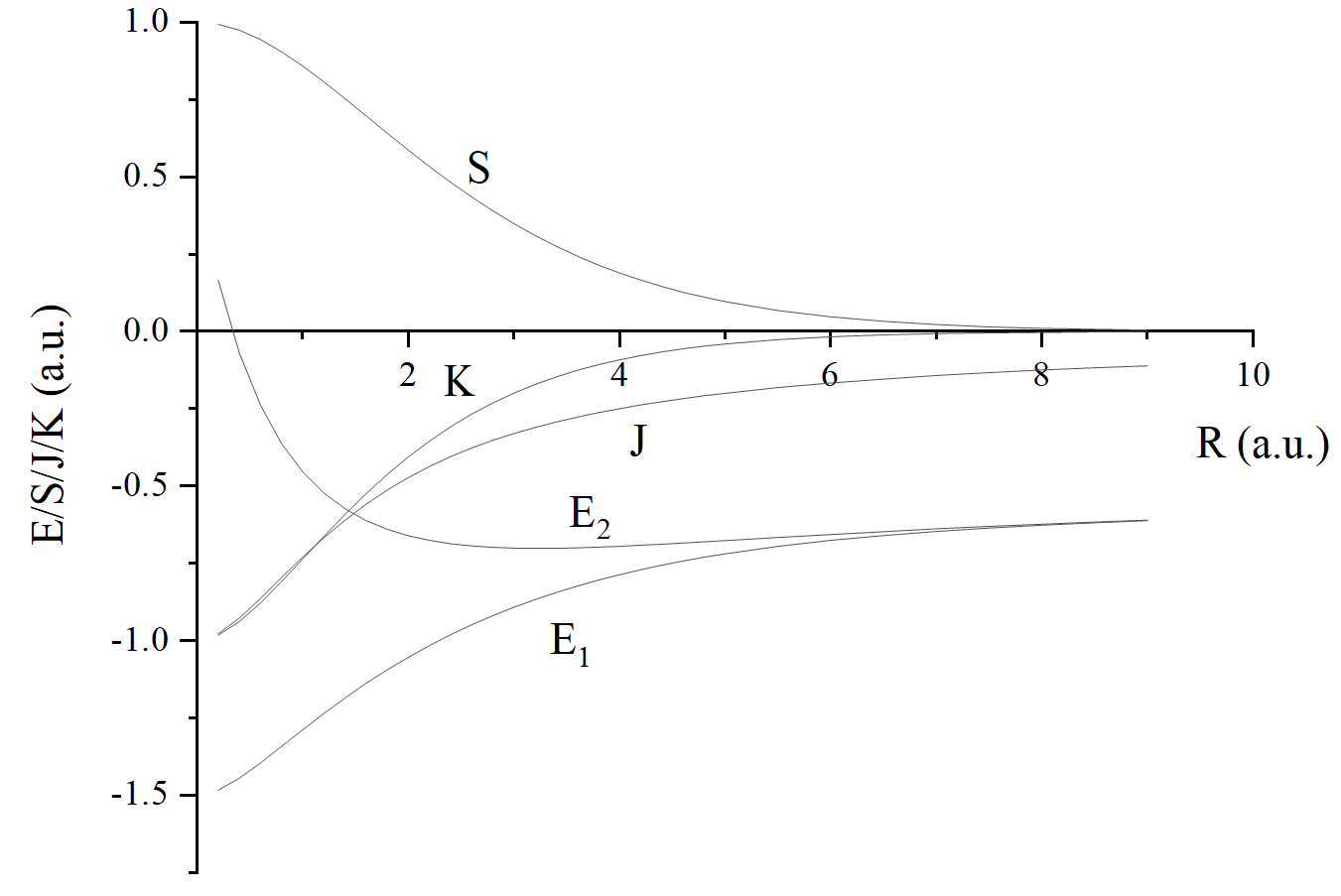
细心的读者会发现怎么反键轨道能量比原子轨道能量还低啊，对于氢分子离子，确实是这样。

进而得到波函数：

$\psi_1=\frac{\phi_1+\phi_2}{\sqrt{2+2S_{12}}}$

$\psi_2=\frac{\phi_1-\phi_2}{\sqrt{2-2S_{12}}}$

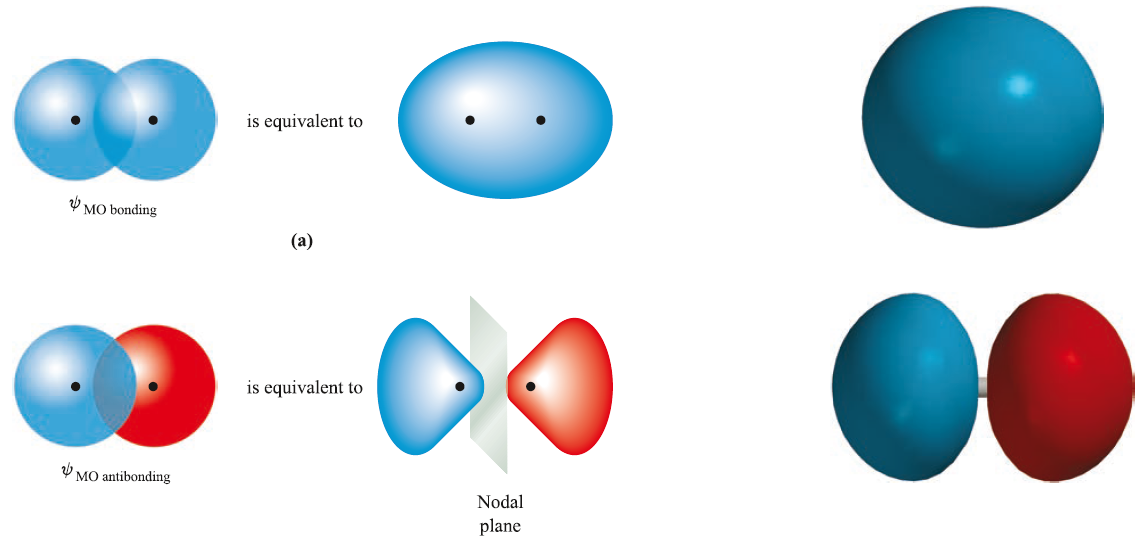
在此基础上加上原子核之间的排斥能 $\frac{1}{R}$ ，总能量曲线如下图所示：

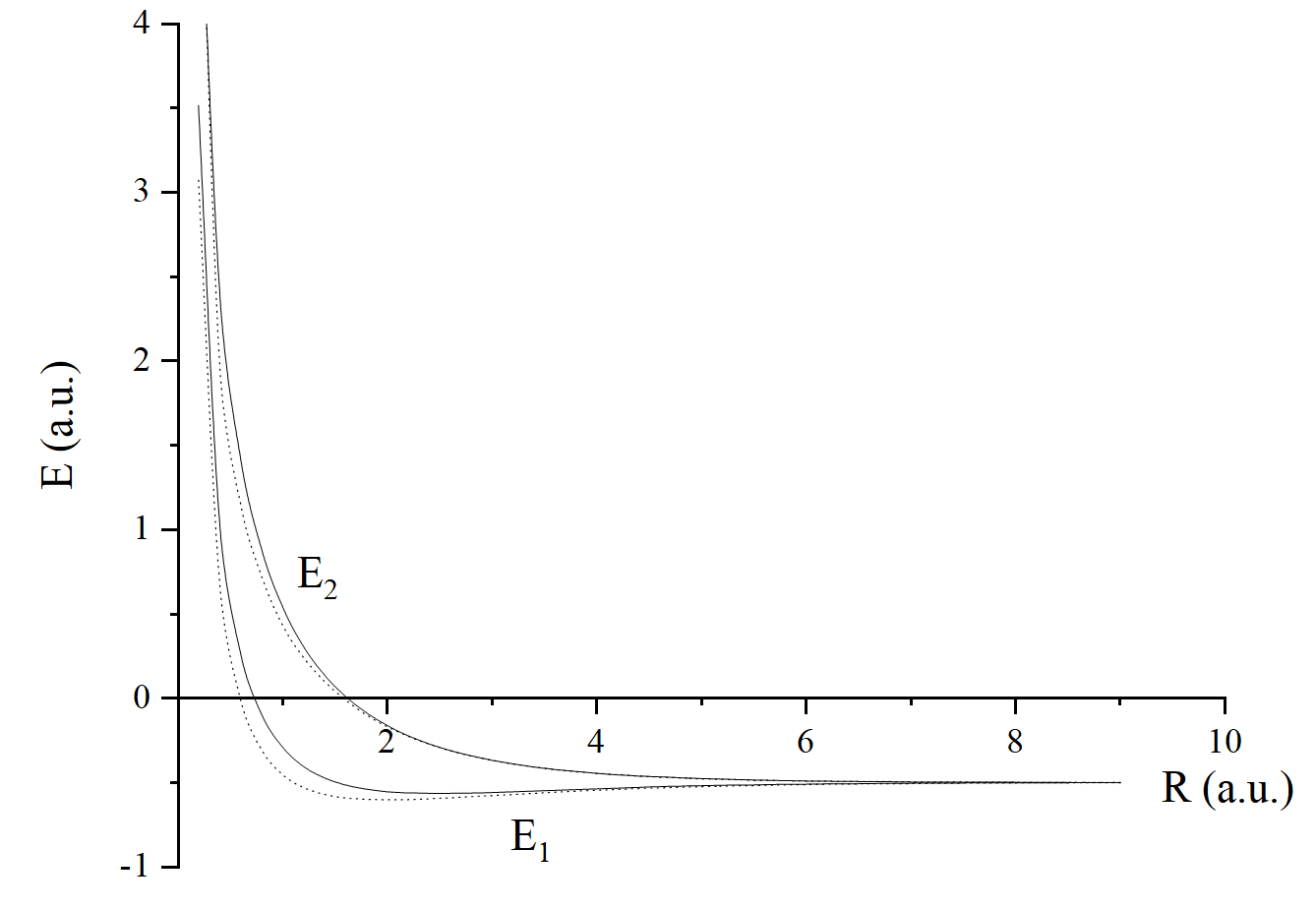
虽然变分法的结果（实线）与精确理论值（虚线）虽然定量上有所误差，但是给出了正确的定性结果。

Slater行列式

现在我们讨论多电子系统。

假设电子之间是没有相互作用的，那么薛定谔方程为：

$(-\sum^{n}_{i=1}\frac12\nabla^2_i-\sum^{n}_{i=1}\sum^{N}_{a=1}\frac{Z_a}{r_{ia}})\Phi=E\Phi$

显然，这是一个可分离变量的方程，分离变量后薛定谔方程可化为上面已经提到过的单电子薛定谔方程：

$\Phi(1,2,...,n)=\psi_1(1)\psi_2(2)...\psi_n(n)$

$(-\frac12\nabla^2_i-\sum^{N}_{a=1}\frac{Z_a}{r_{ia}})\psi_i=\varepsilon_i\psi_i$

完整描述电子，光有分子轨道是不够的，还得乘上自旋波函数 $\eta(s)$ ：

$\chi_i(x)=\psi_i(r)\eta(s)$

于是总波函数变为

$\Psi'(1,2,...,n)=\chi_1(1)\chi_2(2)...\chi_n(n)$

但是这个波函数这是不正确的，因为电子是费米子，具有交换反对称性：

$\Psi(1,2,...,n)=-\Psi(2,1,...,n)$

上面的乘积并不满足这一条件。我们应该通过线性组合使得交换反对称性成立，我们自然而然可以想到，可以用行列式来表示波函数：

$\Psi(1,2,...,n)=\frac{1}{\sqrt{N!}}\begin{vmatrix}\chi_1(1)&\chi_2(1)&\cdots&\chi_n(1)\\\chi_1(2)&\chi_2(2)&\cdots&\chi_n(2)\\\vdots&\vdots&\ddots&\vdots\\ \chi_1(n)&\chi_2(n)&\cdots&\chi_n(n)\end{vmatrix}$

这就是Slater行列式，我们可以表记如下：

$\Psi(1,2,...,n)=\left|\chi_1\chi_2...\chi_n\right>$

库仑积分与交换积分

对于有电子相互作用的系统，我们仍然使用Slater行列式去近似，但是如何寻找 $\{\chi_i(x)\}$ 呢，如何对无相互作用的单电子薛定谔方程进行修正呢？

在回答这个问题之前，我们先看一看有电子相互作用的Slater行列式的能量，B.O.近似去除原子核运动后的哈密顿算符为：

$\hat H=-\sum^{n}_{i=1}\frac12\nabla_i^2-\sum^{n}_{i=1}\sum^{N}_{a=1}\frac{Z_a}{r_{ia}}+\frac12\sum^n_{i=1}\sum^n_{j\ne i}\frac{1}{r_{ij}}$

因此能量为

$E=\left<\chi_1\chi_2...\chi_n \right| \hat H\left |\chi_1\chi_2...\chi_n\right>=\sum^{n}_{i=1}\left+\frac12\sum^{n}_{i=1}\sum^{n}_{j=1}(\left<ij |ij\right>-\left<ij|ji\right>)$

（式中对 $j$ 的求和原本是 $j\ne i$ ，但是因为 $\left<ii |ii\right>-\left<ii |ii\right>=0$ ，所就重写成了 $j=1$ ）

其中，

$\left=\left<\chi_i\right|-\frac12\nabla^2-\sum^{N}_{a=1}\frac{Z_a}{r_{a}}\left |\chi_j\right>$

$\left<mn |pq\right>=\int\chi_m^*(x_1)\chi^*_n(x_2)\frac{1}{r_{12}}\chi_p(x_1)\chi_q(x_2)\ce dx_1\ce dx_2$

因此， $\left$ 代表了无电子相互作用的轨道能量 $h_i$ ， $\left<ij |ij\right>$ 代表了经典的库仑作用，称为库仑积分 $J_{ij}$ ，而 $\left<ij|ji\right>$ 则只有在 $\chi_i$ 和 $\chi_j$ 自旋相同时才不为零，称为交换积分 $K_{ij}$ 。

交换积分体现出了自旋相关效应，自旋相同的电子具有相互远离的倾向，这导致了他们之间的库仑排斥减少，因此在库仑积分的基础上要再减去一个交换积分，这就是说，自旋相同的电子将导致能量降低，这将导出洪特规则。

最后我们将总能量重新写作：

$E=\sum^{n}_{i=1}h_i+\frac{1}{2}\sum^{n}_{i=1}\sum^{n}_{j=1}(J_{ij}-K_{ij})$

实例2：分子轨道理论处理氢分子

显然，用两个原子轨道组成的两个分子轨道为

$\psi_1=\frac{\phi_1+\phi_2}{\sqrt{2+2S_{12}}}$

$\psi_2=\frac{\phi_1-\phi_2}{\sqrt{2-2S_{12}}}$

Slater行列式为：

$\Psi(1,2)=\frac{1}{\sqrt{2}}\begin{vmatrix}\psi_1(1)\alpha(1)&\psi_1(2)\alpha(2)\\\psi_1(1)\beta(1)&\psi_1(2)\beta(2)\end{vmatrix}=\frac{1}{\sqrt2}\psi_1(1)\psi_1(2)[\alpha(1)\beta(2)-\beta(1)\alpha(2)]$

氢分子的电子能量为：

$E=2E_1+J_{11}$

其中 $E_1$ 是氢分子离子的成键分子轨道的能量。注意，此处的 $J_{11}$ 的下标与上一节推导中的下标含义不同，此处的下标是指分子轨道编号，而分子轨道与自旋波函数相乘得到的单电子波函数的编号。

接下来我们稍微探讨一下价键理论和分子轨道理论的关系，将波函数的空间部分拆开可得（以下推导省略归一化系数）：

$\begin{align}\psi_1(1)\psi_1(2)&=[\phi_1(1)+\phi_2(1)][\phi_1(2)+\phi_2(2)]\\&=\phi_1(1)\phi_2(2)+\phi_1(2)\phi_2(1)+\phi_1(1)\phi_1(2)+\phi_2(1)\phi_2(2)\end{align}$

前两项 $\phi_1(1)\phi_2(2)+\phi_1(2)\phi_2(1)$ 正是价键理论的结果，是共价项，而 $\phi_1(1)\phi_1(2)+\phi_2(1)\phi_2(2)$ 则是两个电子全部偏于同一个原子的离子项。

可以预料到，这一波函数在近似两个氢原子的远距离行为时将会变得非常不准确，因为远距离时不应该具有离子项。

这里给大家看看一张HF/STO-3G计算结果和精确值的对比，体会一下这个现象：

图中看似不满足变分原理是因为这是两个值相减的结果。

Fock方程：Slater行列式近似下分子轨道所满足的方程

由上分析可得，一个电子应当除了受到核的吸引、经典的库仑作用外还受到一种自旋相同电子间的交换作用。这样我们直接写出单电子波函数 $\chi_i$ 的近似“薛定谔方程”，其实就是Fock方程（通过变分法推导Fock方程见附录）：

$\left[-\frac12\nabla^2_i-\sum^{N}_{a=1}\frac{Z_a}{r_{ia}}+\sum^n_{j=1}\left(\int\ce dx_j\chi_j^*(x_j)\frac{1}{r_{ij}}\chi_j(x_j)\right)-\sum^n_{j=1}\left(\int\ce dx_j\chi_j^*(x_j)\frac{1}{r_{ij}}\hat P_{ij}\chi_j(x_j)\right)\right]\chi_i(x_i)=\varepsilon_i\chi_i(x_i)$

其中交换算符 $\hat P_{ij}$ 的作用是

$\left[\int\ce dx_j\chi_j^*(x_j)\frac{1}{r_{ij}}\hat P_{ij}\chi_j(x_j)\right]\chi_i(x_i)=\left[\int\ce dx_j\chi_j^*(x_j)\frac{1}{r_{ij}}\chi_i(x_j)\right]\chi_j(x_i)$

简记为：

$[\hat h+\sum_{j=1}^n(\hat J_j-\hat K_j)]\chi_i=\varepsilon_i\chi_i$

进一步简记为

$\hat f\chi=\varepsilon\chi$

将 $\chi$ 去掉自旋波函数 $\eta$ ，就得到了分子轨道（Hartree-Fock轨道） $\psi$ 。

分子轨道的能量为：

$\varepsilon_i=h_i+\sum^{n}_{j=1}(J_{ij}-K_{ij})$

恭喜你，你发现了总能量并不等于分子轨道能量相加：

$E=\sum^{n}_{i=1}h_i+\frac{1}{2}\sum^{n}_{i=1}\sum^{n}_{j=1}(J_{ij}-K_{ij})=\sum^{n}_{i=1}\varepsilon_i-\frac{1}{2}\sum^{n}_{i=1}\sum^{n}_{j=1}(J_{ij}-K_{ij})$

我们仍然可以用一组原子轨道 $\{\phi_i\}$ 的线性组合近似Hartree-Fock轨道 $\psi$ ：

$\psi=\sum_{i=1}^nc_i\phi_i$

同样地线性变分法的最佳近似解是通过求解如下方程得到的：

$(\bold F-ε\bold S)\bm c=0$

其中， $S_{ij}=\left<\phi_i|\phi_j\right>$ ， $F_{ij}=\left<\phi_i\right |\hat f\left |\phi_j\right>$ .

我们将 $n$ 个 $\varepsilon$ 和 $n$ 个系数 $\bm c$ 组合起来写成如下两个矩阵：

$\bold ε=\begin{bmatrix}ε_1\\&ε_2\\&&\ddots\\&&&ε_n\end{bmatrix}$

$\bold C=[\bm c_1,\bm c_2,...,\bm c_n]$

就可以得到Hartree-Fock-Roothaan方程：

$\bold{FC}=\bold{SCε}$

该方程可以通过迭代求得自洽解。

到此为止大家应该完全地理解分子轨道理论了，完结欢呼。

附录

变分原理

设 $\{\psi_i\}$ 是 $\hat H$ 的本征函数集，对于任意归一化的试探波函数 $\Psi$ 可以进行展开：

$\Psi=\sum_{i}^{\infty}{c_i\psi_i}$

因此能量：

$E=\left<\Psi\right|\hat H\left|\Psi\right>=\sum_{i}^{\infty}{c_i^2\varepsilon_i}\geq\sum_{i}^{\infty}{c_i^2\varepsilon_0}=\varepsilon_0$

线性变分法

设试探波函数 $\Psi$ 为一组有限的基函数 $\{\phi_i\}$ 的线性组合

$\Psi=\sum_{i}^nc_i\phi_i$

为了方便讨论，假设系数都是实的。其能量为

$E=\frac{\left<\Psi\right |\hat H\left |\Psi\right>}{\left<\Psi|\Psi\right>}=\frac{\sum_ic_i^2H_{ii}+\sum_{i\ne j}c_ic_jH_{ij}}{\sum_ic_i^2+\sum_{i\ne j}c_ic_jS_{ij}}$

能量取极值时，则能量对于变分参数的偏导数为 $0$ ， $\frac{\partial E}{\partial c_i}=0$ （如果系数是复数，那么对于 $c_i$ 和 $c^*_i$ 的偏导数都要为零）。

先将分母乘到左边，然后求导，得到方程组：

$(c_i+\sum_{i\ne j}c_jS_{ij})E=c_iH_{ii}+\sum_{i\ne j}c_jH_{ij}$

整理为关于系数的方程：

$(H_{ii}-E)c_i+\sum_{i\ne j}(H_{ij}-ES_{ij})c_j=0$

注意到 $S_{ii}=1$ 因此上式可写为：

$\sum_{j=1}^n(H_{ij}-ES_{ij})c_j=0$

综合不同 $\frac{\partial E}{\partial c_i}=0$ 得出的方程，可以写出：

$(\bold H-E\bold S)\bm c=0$

为了使该方程组有非零解，需要系数矩阵的行列式（即久期行列式）为0，因此：

$\det{(\bold H-E\bold S)}=0$

或者直接写出来就是：

这是一个 $n$ 阶行列式，因此是 $E$ 的 $n$ 次方程，因此有 $n$ 个解，对应地，就有 $n$ 套归一化的线性系数 $\bm c$ ，就有 $n$ 个分子轨道。

所以，有几个原子轨道参与组成分子轨道，就有几个分子轨道。

我们知道 $E_i\geq\varepsilon_0$ ，但是在线性变分法中还有 $E_i\geq\varepsilon_i$ ，下面给出证明。

线性变分法中能量极值对应本征能量上界的证明

不妨设基函数 $\{\phi_i\}$ 都是正交的，于是有

$\bold H\bm c=E\bm c$

根据试探波函数能量极值的大小 $E_i$ ，记对应的试探波函数为 $\Psi_i$ ，记本征能量 $\varepsilon_i$ 对应的本质波函数为 $\psi_i$ ，

现在令新的归一化试探波函数 $\Phi_k=\sum_{i=0}^{k}{c_i\Psi_i}$ ，并且满足

$\left<\Phi_k|\psi_i\right>=0,\quad i<k$

将 $\Phi_k$ 用本征波函数展开：

$\Phi_k=\sum_{i=0}^{\infty}{d_i\psi_i}$

有 $d_i=0,\quad i<k$

因此

$\left<\Phi_k\right|\hat H\left|\Phi_k\right>=\sum_{i=k}^{\infty}d_i^2\varepsilon_i\geq\varepsilon_k$

而

$\left<\Phi_k\right|\hat H\left|\Phi_k\right>=\sum_{i=0}^kc_i^2E_i\leq E_k$

故

$E_i\geq\varepsilon_i$

变分法推导Fock方程

Slater行列式 $\Psi(1,2,...,n)=\left|\chi_1\chi_2...\chi_n\right>$ 的能量为：

$E=\sum^{n}_{i=1}\left+\frac12\sum^{n}_{i=1}\sum^{n}_{j=1}(\left<ij |ij\right>-\left<ij|ji\right>)$

我们要求其中的单电子波函数 $\{\chi_i\}$ 都是正交的：

$\left<i|j\right>=\delta_{ij}$

我们用拉格朗日乘数法求 $E$ 的极值：

$L=E-\sum_{i,j}\varepsilon_{ij}(\left<i|j\right>-\delta_{ij})$

极值满足 $\delta L=0$ 。

现在对 $\chi_i$ 添加微扰 $\delta\chi_i$ ，

$\delta\sum^{n}_{i=1}\left=\left<\delta i |h|i\right>+c^*$

$\delta\frac12\sum^{n}_{i=1}\sum^{n}_{j=1}(\left<ij |ij\right>-\left<ij|ji\right>)=\sum^{n}_{j=1}(\left<\delta ij |ij\right>-\left<\delta ij|ji\right>)+c^*$

二分之一系数之所以去掉了，是因为 $\left<\delta ij |ij\right>=\left<j\delta i |ji\right>$ ， $\left<\delta ij|ji\right>=\left<j\delta i|ij\right>$

$\delta\sum_{i,j}\varepsilon_{ij}(\left<i|j\right>-\delta_{ij})=\sum^{n}_{j=1}\varepsilon_{ij}\left<\delta i|j\right>+c^*$

其中每一项的 $c^*$ 为前一项的复共轭。

因此

$\delta L=\int\ce dx_i\delta\chi^*_i(1)\left[\left(-\frac12\nabla^2_i-\sum^{N}_{a=1}\frac{Z_a}{r_{ia}}\right)\chi_i(x_i)+\sum^n_{j=1}\left(\int\ce dx_j\chi_j^*(x_j)\frac{1}{r_{ij}}\chi_j(x_j)\right)\chi_i(x_i)-\sum^n_{j=1}\left(\int\ce dx_j\chi_j^*(x_j)\frac{1}{r_{ij}}\chi_i(x_j)\right)\chi_j(x_i)-\sum^{n}_{j=1}\varepsilon_{ij}\chi_j(x_i)\right]+c^*=0$

由于 $\delta\chi_i$ 是任意的，故

$\left(-\frac12\nabla^2_i-\sum^{N}_{a=1}\frac{Z_a}{r_{ia}}\right)\chi_i(x_i)+\sum^n_{j=1}\left(\int\ce dx_j\chi_j^*(x_j)\frac{1}{r_{ij}}\chi_j(x_j)\right)\chi_i(x_i)-\sum^n_{j=1}\left(\int\ce dx_j\chi_j^*(x_j)\frac{1}{r_{ij}}\chi_i(x_j)\right)\chi_j(x_i)-\sum^{n}_{j=1}\varepsilon_{ij}\chi_j(x_i)=0$

也就是

$\hat f\chi_i=\sum^{n}_{j=1}\varepsilon_{ij}\chi_j$

接下来，通过酉变换 $\{\chi_i\}$ 使 $\boldε$ 对角化即可得到：

$\hat f\chi=\varepsilon\chi$

完结撒花。

可能错误很多但是回答了题主其它问题的原回答

为什么可以用原子轨道线性组合表示分子轨道？

实际上是，因为我们无法解出更大体系的精确解，所以我们考虑先做BO近似和单电子近似，认为总波函数是由分子轨道组成的Slater行列式，然后用原子轨道的线性组合来近似分子轨道。

变分原理告诉我们，试探波函数的能量总是不小于基态能量，而线性变分法则进一步可以得出，解出的第n个能量极值不小于第n个本征态的能量。

所以n个原子轨道线性组合，可以求得n个能量极值，所以就得到n个分子轨道，这些分子轨道就分别用来作为真实本征态的近似。

更新：评论区大佬指出我上一句话“完全不对”，或许我应该说n个原子轨道线性组合按照变分法可得到n个近似分子轨道，作为准确分子轨道的近似？

以及轨道在坐标系中一定要取得四四方方么？比如对于甲烷，我们放好四个H之后歪着摆上C的原子轨道，那么得到的结果还是三重简并态么？

把原子轨道重新线性组合一下就可以得到摆正但仍然正交的轨道了。

以及确定形状的分子的轨道是一定的么？

综上，因为分子轨道是要求满足其为试探波函数的能量的极值，因此是一定的。

更新：仔细一想，氧分子中的π分子轨道可以“乱转”，这个是要看对称性。

推荐一些合适的书籍

先去找本《结构化学》看，然后学学线性代数后看看格里菲斯《量子力学概论》、Szabo & Ostlund, Modern Quantum Chemistry等等。

另外还有赖文《量子化学》、徐光宪等《量子化学》、Albright et el., Orbital Interactions in Chemistry