OpenMolcas计算SO-NTO 以及 NTO对的可视化

叫个啥名字发布于 2022-5-28 16:40 阅读：568 linux

OpenMoclas22.02版本已经支持SO-NTO的计算

1.计算方法

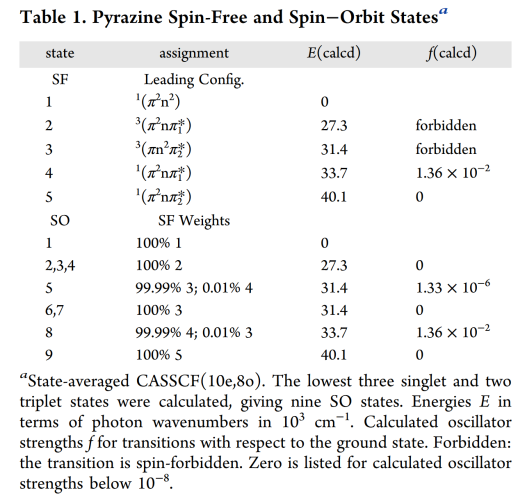
本文以pyrazine分子为例，使用的OpenMoclas版本为V22.02。CASSCF计算选取8个活性轨道CAS(10,8), 活性轨道在下图所示。利用态平均方法共计算3个singlet以及3个triplet。在计算旋轨耦合时，triplet仅选取最低的两个态进行SO计算。3个singlet与2个triplet共产生9个SO态。软后选取特定的轨道跃迁进行SO-NTO分析。

2.输入文件

&SEWARD
Title
Calculation for pyrazine S0 geometry
cholesky
BSSHOW
Basis set
H.ANO-DK3.Tsuchiya.6s.1s.
H1 1.2556 -2.0749 0 ANGSTROM
H2 -1.2581 -2.0734 0 ANGSTROM
H3 1.2581 2.0734 0 ANGSTROM
H4 -1.2556 2.0749 0 ANGSTROM
End of basis
Basis set
C.ANO-DK3.Tsuchiya.12s7p.2s1p.
C1 0.6985 -1.1333 0 ANGSTROM
C2 -0.6999 -1.1325 0 ANGSTROM
C3 0.6999 1.1325 0 ANGSTROM
C4 -0.6985 1.1333 0 ANGSTROM
End of basis
Basis set
N.ANO-DK3.Tsuchiya.12s8p.2s1p.
N1 1.4173 -0.0008 0 ANGSTROM
N2 -1.4173 0.0008 0 ANGSTROM
End of basis
AMFI
ANGMOM
0.0 0.0 0.0
RELAtivistic
R03O03
End of input

&SCF

&RASSCF
Title = The CASSCF of pyrazine with an active space of (10,8)
Spin
1
Symmetry
1
NACTel
10 0 0
Inactive
16
RAS2
8
TypeIndex
CIRoots
4 4 1
Iter
100 100
LUMORB
orbappear
compact
OUTOrbitals
CANONIcal
All
End of input

>>> COPY $Project.JobIph $Project.JobIph.s0s1s2s3
>>> COPY $Project.RasOrb.1 $Project.RasOrb.s0
>>> COPY $Project.RasOrb.2 $Project.RasOrb.s1

&RASSCF
Title = The CASSCF of pyrazine with an active space of (10,8)
Spin
3
Symmetry
1
NACTel
10 0 0
Inactive
16
RAS2
8
TypeIndex
CIRoots
3 3 1
Iter
100 100
LUMORB
orbappear
compact
OUTOrbitals
CANONIcal
All
End of input
>>> COPY $Project.JobIph $Project.JobIph.t1t2t3
>>> COPY $Project.RasOrb.1 $Project.RasOrb.t1
>>> COPY $Project.RasOrb.2 $Project.RasOrb.t2

>>> COPY $Project.JobIph.s0s1s2s3 JOB001
>>> COPY $Project.JobIph.t1t2t3 JOB002

&RASSI
NTOC
NrofJobIphs
2 3 2
1 2 3
1 2
SPINorbit
DIPR
1.0D-15
SONT
2
1 5
5 8
MEES *print over SF states
MESO *print over SO states
End of input

3.结果分析

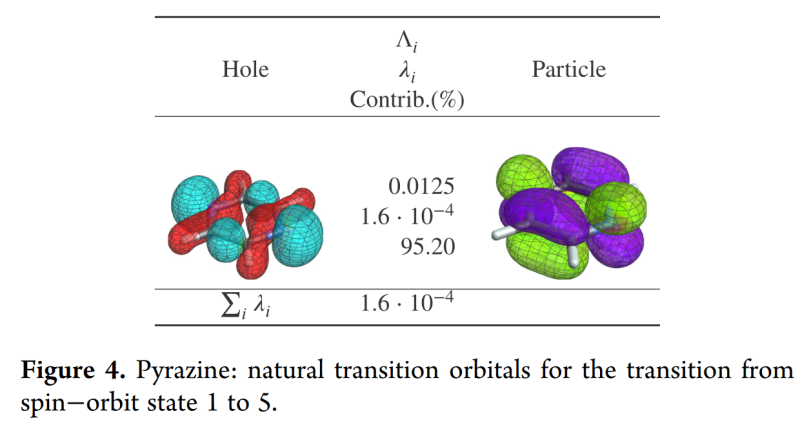
下图是SO态1-5的跃迁NTO

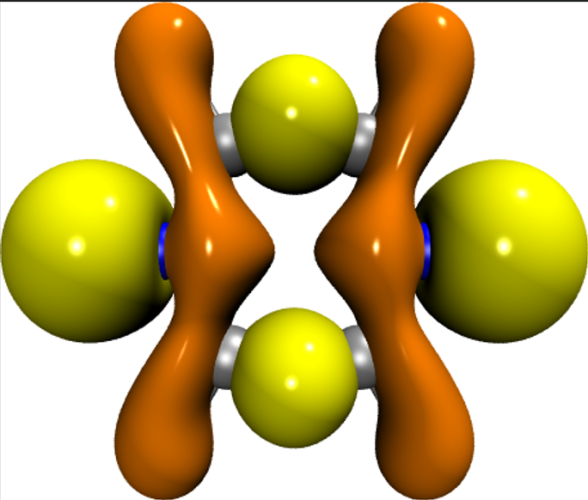
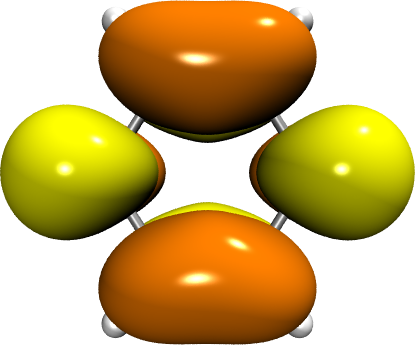
轨道以及数值与本人计算结果基本一致，以下是我的计算结果以及NTO对

==========================================================================================
EXCITATION EIGENVALUE EXCITATION TRANSITION DIPOLE MOMENT
AMPLITUDE CONTRIBUTION(%) (1) (2) (3)
------------------------------------------------------------------------------------------
0.01293 0.00017 95.49 -0.0000-0.0000i 0.0000+0.0000i 0.0000+0.0029i
0.00274 0.00001 4.30 -0.0000-0.0000i 0.0000+0.0000i 0.0000+0.0011i
0.00051 0.00000 0.15 0.0000+0.0000i 0.0000+0.0000i -0.0000-0.0001i
0.00032 0.00000 0.06 -0.0000-0.0000i -0.0000-0.0000i -0.0000-0.0001i
SUM OF EIGENVALUES 0.00018
SUM OF TRANSITION DIPOLE -0.0000-0.0000i -0.0000-0.0000i 0.0000+0.0037i
==========================================================================================

HOLE

PART

Λ在文中的表达是amplitude (singular value) 振幅（奇异值）

λ是eigenvalue (square of the amplitude) 特征值（振幅的平方）

contribution (“Contrib.”) is the ratio of the corresponding eigenvalue and the sum of all eigenvalues 相应的特征值占比，对应的数值为输出文件中的占据数。

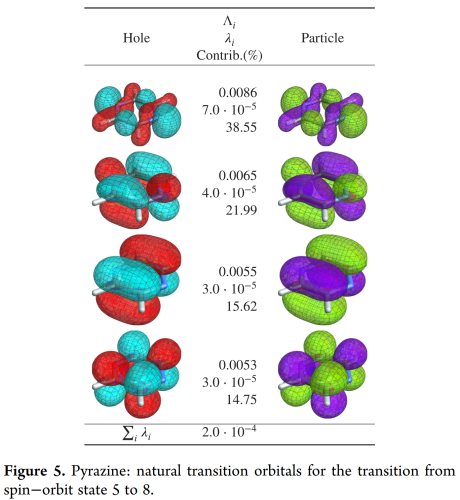
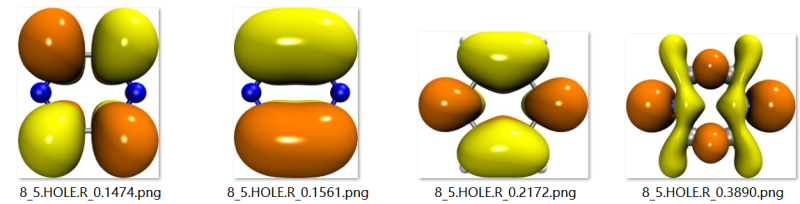
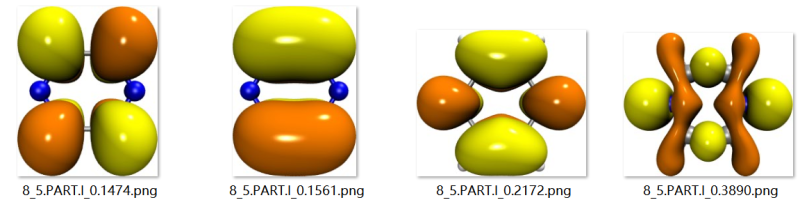
下图是SO态5-8的跃迁NTO

轨道以及数值与本人计算结果基本一致，以下是我的计算结果以及NTO对

==========================================================================================
EXCITATION EIGENVALUE EXCITATION TRANSITION DIPOLE MOMENT
AMPLITUDE CONTRIBUTION(%) (1) (2) (3)
------------------------------------------------------------------------------------------
0.00893 0.00008 38.90 -0.0000+0.0000i 0.0000-0.0000i -0.0000+0.0000i
0.00667 0.00004 21.72 0.0000-0.0000i 0.0000-0.0000i -0.0000+0.0000i
0.00566 0.00003 15.61 0.0000-0.0000i -0.0000+0.0000i -0.0000+0.0000i
0.00550 0.00003 14.74 0.0000-0.0000i -0.0000+0.0000i 0.0000-0.0000i
0.00387 0.00001 7.29 -0.0000+0.0000i 0.0000-0.0000i -0.0000+0.0000i
0.00157 0.00000 1.21 0.0000-0.0000i 0.0000-0.0000i -0.0000+0.0000i
0.00083 0.00000 0.34 -0.0000+0.0000i 0.0000-0.0000i 0.0000-0.0000i
0.00062 0.00000 0.19 -0.0000+0.0000i 0.0000-0.0000i 0.0000-0.0000i
SUM OF EIGENVALUES 0.00021
SUM OF TRANSITION DIPOLE -0.0000+0.0000i -0.0000+0.0000i -0.0000+0.0000i
==========================================================================================

HOLE

PART

输出文件 pyrazine.zip

4.轨道可视化

结合Multiwfn以及MOKIT将inporb转为molden，然后利用vmd并编写的脚本进行轨道批量可视化。

详情可见前面讨论的inporb转为molden。

本文数据以及输入文件均来自 Feng, Rulin, Xiaojuan Yu, and Jochen Autschbach. “Spin–Orbit Natural Transition Orbitals and Spin-Forbidden Transitions.” Journal of Chemical Theory and Computation 17, no. 12 (December 14, 2021): 7531–44. https://doi.org/10.1021/acs.jctc.1c00776.

另外有一篇写的较好的NTO的博文。

OpenMolcas SONTO