量子化学计算中的交换相关能
1.多体系统的薛定谔方程求解
量子化学的本质是求解薛定谔方程,多体体系的哈密顿量如下:

包括五项: (1)电子动能,(2)原子核动能,(3)原子核与电子之间的库伦势能,(4)电子与电子之间的库伦势能,(5)原子核与原子核之间的库伦势能。分子是含有多个核与电子的体系,其薛定谔方程的求解是一个极为困难的问题。为了能直观的感受,假设我们想计算拥有8个电子的氧原子的波函数。若不考虑自旋,波函数与24个坐标有关。我们大概需要多少数据去完整的刻画这个系统呢?假设每个坐标用10个数表示,则我们总共需要10^24个数。若每个数占据一个字节,那就是10^24个字节的数据量。将这些数据存入质量10g,数据容量519^9个字节的DVD光盘中,则我们需要的DVD总量就达到了10^9吨!这还仅仅只是进行数据存储,若是进行进一步的处理,只会更加麻烦。
于是,我们就有必要引入若干的近似和方法,它们逐级列举如下:
(1)波恩奥本海默近似
由于核的质量比电子质量大得多,核的运动比电子运动慢得多,因此核的运动与电子运动可以分开处理。处理电子运动时,认为核是固定不动的。处理核运动时,认为电子的快速运动建立一个平均化了的负电荷分布,核在这样一个负电荷势场中运动。因此,我们将原子核“冻结”在固定点处,从而可以忽略它们的运动。我们因此略去原子核的动能以及核与核的相互作用项,也就是第二项和第五项。此时对于整个多电子体系来说,原子核分布就相当于提供了某种“外场”,于是哈密顿量剩下三项:电子动能,电子势能,原子核与电子的势能。
(2)Hartree-Fock近似
经过以上简化以后哈密顿量变得相对简单,电子动能和原子核与电子的势能是单体项,容易求解。但是电子势能是二体项,绝大多数理论的开头就是想办法在这一项上做文章,想办法干掉这一项。这里想到的一个方法就是平均场近似,认为电子电子的相互作用并不是瞬时的,而是每个处在其他电子的平均场中。在这个近似中,多电子波函数是以单电子波函数的斯莱特行列式的形式出现的,将其代入多体薛定谔方程并进行平均场近似就可以得到如上单体的Hartree-Fock方程,这是一种单电子近似的方法。显然,在这个近似下的哈密顿量是不准确的。比如电子电子相互作用被涵盖在平均场里面,但是每个电子间的相互作用确是重复计算了的。
2.交换关联能介绍
2.1电子的交换与关联
Hartree的方法求到的总能量与实验值相比误差太大,原因是总波函数不等于单电子波函数的乘积。电子要满足全同性和反对称性,即所有电子无法区分,任意交换两个电子的位置,波函数要加负号。为了满足全同性和反对称性,Fock构造出Slater行列式来描述点电子波函数,行列式交换任意两行或两列,行列式的值都会变负,这一部分能量被称为交换能。
关联势能是指体系中自旋相反的电子相互作用之后得到的能量,这部分能量含有多种势能,比较复杂。
2.2电子关联与HF方法的缺陷
电子实际上并不能独立地运动,由于库仑排斥,一个电子禁止其他电子靠近,这称为电子运动相关或关联。
HF理论采用单行列式波函数,它考虑了同自旋电子的运动关联,但不考虑不同自旋的电子之间的运动关联,认为不同自旋的电子可以靠得很近,这将高估电子间相互作用能,产生误差。
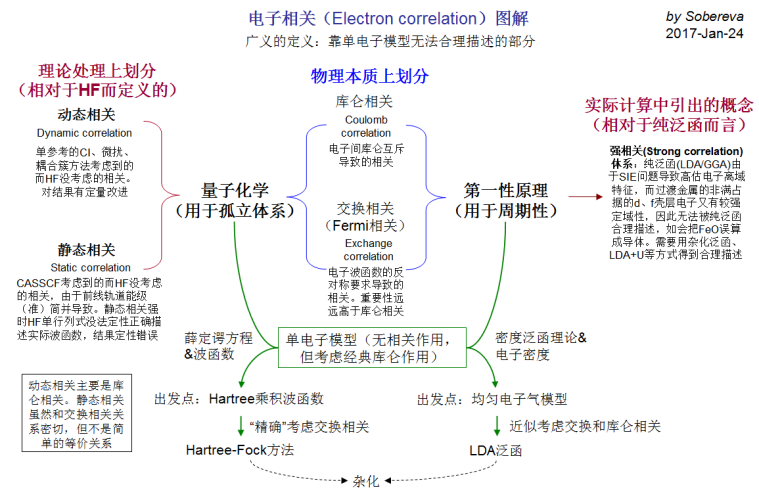
2.sob的一张ppt很好的总结了量化中的动态,静态相关
sob的这张ppt中讲到静态相关与动态相关在不同的领域解释不同,在第一性原理与量子化学中的解释有些许差别。
3.一些量化工作者的回答
我并不是很喜欢区分量子化学和第一性原理这样的词汇,姑且叫做原子分子与固体中概念差异吧,我觉得这是个有趣的问题,我把我对这些问题的认知说一下,当然不见得全都是正确的理解,大家也不妨讨论下:
1、原子分子中电子关联的概念和固体上的定义有啥不同?
实际上是因为零级近似的取法不同导致的一些“观念”上的差异,习惯上固体上更常使用近自由电子近似而并非把系统的态写成Slater行列式,这大体就是Hartree近似的级别,因此两种“关联”作用——交换(Fermi关联)、关联(Coulomb关联)作用都未被包含,这些作用通通定义为关联作用。而按照post-HF的观念来看,HF已经包含了一定的交换作用,剩余没有描述的作用定义为关联作用。
2、为啥固体计算中不把Slater行列式作为零级近似?
(1)历史遗留问题,也是唯象上说,自由电子气模型足够接近金属,并且足够简单。
(2)按照原子分子中对关联作用的定义来说,金属性强的系统静态关联比较强,Fermi能级附近的能级是准连续的,价带导带直接接在一块儿,我们知道,这种情况Hartree-Fock一定是failed的。计算结果来说确实如此,就是能把金属算成有带隙的,Si的带隙是10eV之类的问题。当然相对而言很多绝缘系统用Hartree-Fock结果还是可以接受的,但这导致应用相当受限。
3、我们能否通过post-HF来消除上述困扰?
原则上来说当然是可以的,处理静态关联那一套来说,我们搞量子化学的当然很清楚。不过在此之前我们必须估计一下计算量,因为不同于原子、分子这样的有限系统,固体是个无限的系统,尽管对k点是有限的采样来求解本征方程,如果在考虑多组态的问题,计算量就非常恐怖了。就拿耦合簇法说,Kresse(VASP)前些年发过计算LiH的CCSD计算,大概目前也就能算这样的系统。
4、强关联效应会引起什么样的问题?
习惯上,多粒子系统的计算通常还是先使用平均场近似,如果平均场fail的话,再进行post修正关联作用,比较常规的方案便是微扰修正。微扰法本身也有适用范围,如果微扰项不足够小,后果就是微扰能发散,这种就是强关联的情况。量子化学里面,Hartree-Fock作为零级函数的微扰方法大家再熟悉不过的就是n阶Möller-Plesset法,自然不适用于静态关联较强的系统。解决问题的思路也很清晰,要么采用非微扰方法,如Quantum Monte Carlo之类,要么零级近似就尽可能包含足够多的关联作用,使得微扰项足够小来避免发散,然后再做微扰,CASPT、GWA这类如此。
5、Hubbard模型到底是描述了什么?
如果简单点说,Hubbard模型相当于Hartree-Fock的单中心近似版本,其中的关联自然是较与近自由电子气近似而言的。DFT+U应当被认为是Hubbard模型在Kohn-Sham框架下的一种近似的实现。近些年,比较流行的看法就是把DFT+U理解为一种自作用修正(SIC)的方式,大体上的原理就是使得通过约束价带电子满足Janak定理来参量U的值。但DFT+U涉及到的具体问题还是很多的